SEGA Genesis: Mandelbrot

Polish-American mathematician Benoit Mandelbrot coined the term 'fractal' in his 1975 book 'Objets Fractals', describing geometric shapes with infinite details. Four years later, he would plot a specific fractal, now known as the 'Mandelbrot Set' on an IBM computer. This formula would fascinate mathematicians and programmers all over the world, and would end up on the cover of Scientific American in August 1985.
Hobby programmers would find that the Mandelbrot Set was relatively easy to plot, and the fractal would end up on the screen on many computers.
In this article, we will look at an implementation of the Mandelbrot set plot in MC68000 assembly code. This is an excellent example to use with one of the Raster Graphics implementations.
Mandelbrot Algorithm
Here is the Mandelbrot rendering algorithm from Wikipedia:
for each pixel (Px, Py) on the screen do
x0 := scaled x coordinate of pixel (scaled to lie in the Mandelbrot X scale (-2.00, 0.47))
y0 := scaled y coordinate of pixel (scaled to lie in the Mandelbrot Y scale (-1.12, 1.12))
x := 0.0
y := 0.0
iteration := 0
max_iteration := 1000
while (x*x + y*y ≤ 2*2 AND iteration < max_iteration) do
xtemp := x*x - y*y + x0
y := 2*x*y + y0
x := xtemp
iteration := iteration + 1
color := palette[iteration]
plot(Px, Py, color)
It's as simple as it gets.
Now, planning the SEGA Genesis implementation, we have to deal with the fact that the MC68000 of the SEGA Genesis does have a floating point unit. The Mandelbrot rendering algorithm doesn't work with integers.
Fixed point numbers are an alternative to floating point numbers that work very well on the Genesis. They are less flexible than floating point numbers, but they perform very well on the MC68000 and are very easy to implement. For now, I will defer to the excellent introduction to fixed point numbers on plutiedev.com.
Fixed-point Mandelbrot in C++
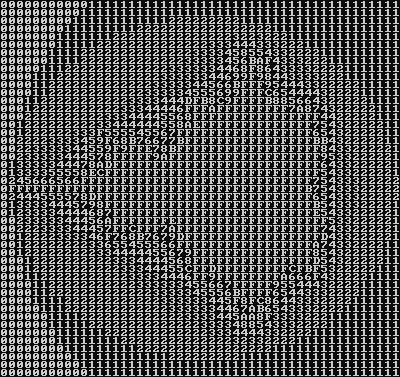
Here is a C++ program that outputs the Mandelbrot set as an array of numbers. It is based on a fixed-point Mandelbrot algorithm by Bernhard Fischer:
#include <cstdio>
#include <cstdint>
typedef int16_t INT;
const int MAX_ITER = 15;
// Based on integer Mandelbrot by Bernhard Fischer
// https://www.cypherpunk.at/2015/10/calculating-fractals-with-integer-operations/
//
INT iterate(int real0, int imag0)
{
const INT NORM_BITS = 6;
const INT NORM_FACT = 1 << NORM_BITS;
INT realq, imagq, real, imag;
INT i;
real = real0;
imag = imag0;
for (i = 0; i < MAX_ITER; i++)
{
realq = (real * real) >> NORM_BITS;
imagq = (imag * imag) >> NORM_BITS;
if ((realq + imagq) > (4 * NORM_FACT))
break;
imag = ((real * imag) >> (NORM_BITS - 1)) + imag0;
real = realq - imagq + real0;
}
return i;
}
int main()
{
const char aa[] = "0123456789ABCDEF";
const INT WIDTH = 256;
const INT HEIGHT = 200;
char line[WIDTH+1];
for (INT y = 0; y < HEIGHT; ++y)
{
for (INT x = 0; x < WIDTH; ++x)
{
INT mx = x-(WIDTH/2)-20;
INT my = y-(HEIGHT/2);
INT iteration_count = iterate(mx, my);
line[x] = aa[iteration_count];
}
line[WIDTH] = 0;
puts(line);
}
int c = getchar();
}
The C++ implementation works with 10.6 bit fixed point numbers (10 bits integral part, 6 bit fractional part). The output is primitive, but the shape of the Mandelbrot set can be clearly noticed in the screenshot to the right.
This C++ implementation is suitable for conversion to MC68000 assembly code.
MC68000 Fixed Point Implementation
; Memory Map
MANDELBROT_ADDR EQU $E0FF00 ; 12 B - 'iterate' stores current config here
iterations EQU (MANDELBROT_ADDR+0)
norm_bits EQU (MANDELBROT_ADDR+4)
norm_bits_minus_1 EQU (MANDELBROT_ADDR+8)
norm_fact EQU (MANDELBROT_ADDR+12)
WIDTH EQU 320
HEIGHT EQU 224
MAX_ITER EQU 15 ; color values between 0 and 15
lea $FF000000,sp
; Render Mandelbrot set to framebuffer address in a0
; a0: framebuffer ptr
; d0: offset x
; d1: offset y
; d2: zoom
; d3: screen y
; returns: updated a0
mandelbrot
movem.l d0-d7/a1-a6,-(sp) ; push all registers to stack
; for each pixel (d6, d7) = (Px, Py) on the screen do
move.w d0,d3
move.w d1,d4
move.w d2,d5
move.w #HEIGHT-1,d7 ; d7: y
next_row
move.w #WIDTH-1,d6 ; d6: x
next_2pixels
move.w d7,d1 ; INT my = y-(HEIGHT/2);
sub.w #HEIGHT/2,d1
move.w d6,d0 ; INT mx = x-(WIDTH/2);
sub.w #WIDTH/2,d0
add.w d3,d0 ; real
add.w d4,d1 ; imag
move.w d5,d2 ; zoom
jsr iterate ; d0 = iteration count
; render d0 to screen here
dbra d6,next_2pixels
dbra d7,next_row
movem.l (sp)+,d0-d7/a1-a6 ; push all registers to stack
rts
; d0: real0
; d1: imag0
; d2: zoom
; d0: return color (0-15)
iterate
movem.l d1-d7,-(sp) ; push all registers to stack
; set up RAM state
move.w d2,(norm_bits) ; NORM_BITS
sub.w #1,d2
move.w d2,(norm_bits_minus_1) ; NORM_BITS-1
move.w #8,d3 ; 4 * (1<<NORM_BITS)
asl.w d2,d3
move.w d3,(norm_fact)
; d0: real0
; d1: imag0
clr.l d2 ; d2: realq
clr.l d3 ; d3: imagq
clr.l d4 ; d4: real
; d5: imag
; d6,d7: temp
move.w d0,d4 ; real = real0
move.w d1,d5 ; imag = imag0
move.l #MAX_ITER-1,d7 ; MAX_ITER
.next
move.l d7,(iterations)
move.w d4,d2 ; realq = (real * real) >> NORM_BITS
muls.w d4,d2
move.w (norm_bits),d6
asr.l d6,d2
move.w d5,d3 ; imagq = (imag * imag) >> NORM_BITS
muls.w d5,d3
move.w (norm_bits),d6
asr.l d6,d3
move.w d2,d6 ; if ((realq + imagq) > 4 * NORM_FACT)
add.w d3,d6 ; break;
cmp.w (norm_fact),d6
bgt done
muls.w d4,d5 ; imag = ((real * imag) >> (NORM_BITS - 1)) + imag0;
move.w (norm_bits_minus_1),d6
asr.l d6,d5
add.w d1,d5
move.w d2,d4 ; real = realq - imagq + real0;
sub.w d3,d4
add.w d0,d4
move.l (iterations),d7
dbra d7,.next
done
move.l (iterations),d7
and.w #$1F,d7
move.w d7,d0
movem.l (sp)+,d1-d7 ; push all registers to stack
rts
You can then call the mandelbrot subroutine like this:
move.w #-70,d0 ; x
move.w #0,d1 ; y
move.w #7,d2 ; zoom
jsr mandelbrot
Easy68K Test Implementation
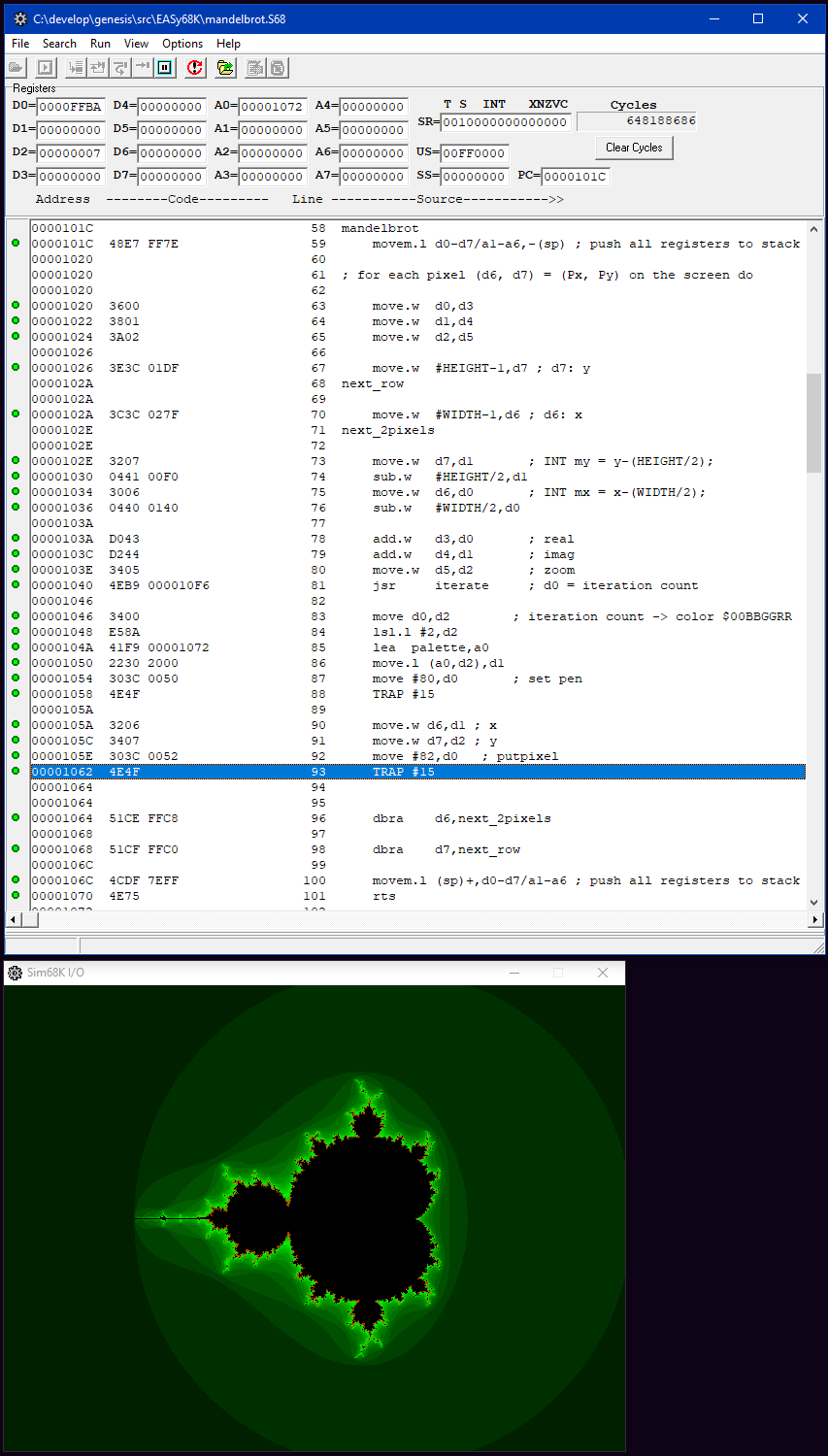
Easy68K is a MC68000 emulator. It is not an emulation of the SEGA Genesis or any other platform, but it is useful for stepping through assembly code. It even has text and graphics output functionality, which can be used to test the Mandelbrot implementation without focusing on SEGA Genesis specifics.
In Easy68K, your code can use the instruction TRAP #15 to access pixels directly in a graphical window. The code is simple enough, if D6 and D7 contains the screen x and y-coordinates, and the iteration count is in D0, the following will put a yellow pixel on 10,10:
move.l #$0000FFFF,d1 ; color $00BBGGRR
move #80,d0 ; set pen color D1
TRAP #15
move.w #10,d1 ; x
move.w #10,d2 ; y
move #82,d0 ; putpixel(D1,D2)
TRAP #15
The result can be seen in the screenshot
SEGA Genesis Implementation
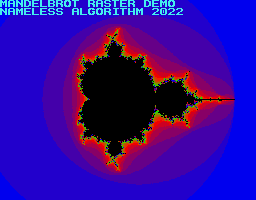
(I seem to have flipped the X-axis)
The SEGA Genesis implementation serves as a demo for the linear bitmap framebuffer explained in the previous article. The returned iteration count is simply written to main RAM, and then copied to VRAM using copy_framebuf.
References
SEGA2.DOC - VDP information and terminology