SEGA Genesis: Structure
Assembly language being lower level than other programming languages makes it very structurally open. It's an interesting language for a computer scientist to work with, as it's open for implementation of any existing or new programming paradigm.
In the following, approaches to variables and types on the Genesis will be discussed, as well as subroutine calling conventions, and an example approach to implementing the State Pattern.
Variables
In assembly code, a variable can be represented by a register or a memory location. The Motorola 68000 has 15 normal registers D0-D7 and A0-A6 (A7 is used as the stack pointer), which will work nicely for local variables in subroutines:
move.w #$7,d0 ; int x = $7
move.w #$F000,d1 ; int y = $F000
add.w d0,d1 ; y += x
lea str,a0 ; char *s = str
move.b (a0),d2 ; char c = *s
Global variables are useful to represent the game state, and are most easily implemented using a fixed memory location. Here is one way to declare a variable in memory:
; note: my_value will be a constant on a Genesis
my_value:
ds.w 7 ; int my_value = 7
The variable will be located in memory next to the code, which should work fine on architectures where the program is loaded into RAM. However, when making a SEGA Genesis ROM, the code is located in read-only memory (ROM) on the cartridge. If my_value is in ROM, it can never be changed and will thus be constant.

If you want a mutable variable, you need to place it in RAM instead. A naive attempt could be to place it in address 0:
; note: my_value will be a constant on a Genesis
my_value = $00000000
move.w #7,my_value ; my_value = 7 ?
This would have worked if address 0 was in RAM on a Genesis, but it isn't. From Charles MacDonald's 'Sega Genesis hardware notes' we can get a memory map of the Genesis, where it becomes clear that address 0 is in ROM:
$000000-$3FFFFF : ROM
$400000-$7FFFFF : Unused (1)
$800000-$9FFFFF : Unused (2)
$A00000-$A0FFFF : Z80 address space (3)
$A10000-$A1001F : I/O
$A10020-$BFFFFF : Internal registers and expansion (4)
$C00000-$DFFFFF : VDP (5)
$E00000-$FFFFFF : RAM (6)
Becase address 0 is in ROM, my_value in the above example is a constant. Our work RAM is in the address space $E00000-$FFFFFF (that's 2 MB). The Genesis only has 64 KB RAM ($10000), but the memory is repeated over and over again in the address space. We can just limit ourselves to using $E00000-$E0FFFF.
So this works:
my_value = $E00000
move.w #7,my_value ; my_value = 7
Using the RAM address space, we can build a memory map of global variables, accessible from any part of our program:
mode = $E00000 ; 2B
xoff = $E00002 ; 2B
yoff = $E00004 ; 2B
str = $E00006 ; 32B string
input = $E00026 ; 1B
With this approach, avoiding variables overlapping in memory is done manually, and must be handled carefully to avoid variables overwriting each other.
In the above example, I reserved 32 B for the str variable, which can be interpreted as an array of 32 single characters. Arrays are discussed in further detail in the upcoming section.
Arrays
Arrays is a key feature in most languages, and absolutely essential for game developement. MC68000 assembly code has no array concept, but arrays are easy to represent and can be accessed through constant indexes or pointers.
Let's re-use the character array str from the previous section:
str = $E00006 ; 32 B string
; in memory: $E00006 - $E00025
We can access any character using a constant index:
lea str,a0
move.b 0(a0),d0 ; d0 = str[0]
move.b 1(a0),d1 ; d1 = str[1]
The addressing mode used here is called Address register indirect with displacement, the 'displacement' being the constant index in front of (a0).
An alternative is to not use displacement, but instead update the address register a0, known as pointer arithmetic:
lea str,a0
move.b (a0),d0 ; d0 = *str (str[0])
add.l #1,a0 ; str++
move.b (a0),d0 ; d0 = *str (str[1])
Structures

The C language has the concept of a structure, a collection of variables that are closely related and next to each other in memory. The widely used concept of classes is an extension of the structure concept: a structure with an accompanying set of functions that all accept a pointer to a structure as their first argument. In high-level languages, this structure pointer (often called this) is usually automatically added to non-static functions as the first argument by the compiler, so programmers do not need to add it manually.
The structure concept is useful in game programming, especially when dealing with large numbers of very similar objects, such as enemies or bullets.
Any set of related variables could be considered an instance of a structure. So if we have a structure representing the position and velocity of an enemy in a game, we could have a structure like this:
; struct enemy
enemy_x = $E00100 ; int16 x
enemy_y = $E00102 ; int16 y
enemy_dx = $E00104 ; int16 dx
enemy_dy = $E00106 ; int16 dy
However, if we want more than one enemy at a time, it would be useful to have an array of structures. In the case of enemy, we could allocate a pool of enemy instances and update all of them every frame.
Array of Structures: Sequential Layout
An obvious way to store an array of enemy structs in memory would be sequentially, like this:
Structure sequence
enemy 0 enemy 1 enemy 2 enemy N
base+$00 base+$08 base+$10 base+N*8
x,y,dx,dy x,y,dx,dy x,y,dx,dy ... x,y,dx,dy
For this, we need to access the structs through a pointer to the beginning of a struct in memory and offsets that represent the different member variables:
enemy_data = $E00100 ; struct enemy [N], takes up N*8 B of memory
offset_x = 0 ; int16 x
offset_x = 2 ; int16 y
offset_dx = 4 ; int16 dx
offset_dy = 6 ; int16 dy
STRUCT_SIZE = 8 ; sizeof(enemy)
If we consider this simple update routine:
for each enemy E
E.x += E.dx
E.y += E.dy
We could implement it like this:
lea enemy_data,a0 ; i = 0; enemy e = data[i]
move.w #N-1,d7
.loop ; do
move.w offset_dx(a0),d0 ; e.x += e.dx
add.w d0,offset_x(a0) ;
move.w offset_dy(a0),d0 ; e.y += e.dy
add.w d0,offset_y(a0) ;
add.l #STRUCT_SIZE,a0 ; e = data[++i]
dbra d7,.loop ; while (i < COUNT)
Next, we will consider an alternative approach to the sequential structure layout.
Array of Structures: Member Arrays
As an alternative to the sequential memory layout, we could store arrays of each member of enemy:
Member array
enemy x: base+$00
x0,x1,x2, ... xN
enemy y: base+N*2
y0,y1,y2, ... yN
enemy dx: base+(N+1)*2
dx0,dx1,dx2, ... dxN
enemy dy: base+(N+2)*2
dy0,dy1,dy2, ... dyN
The update algorithm:
for each enemy E
E.x += E.dx
E.y += E.dy
Could be implemented using the member array approach:
lea enemy_x,a0 ; int16 *enemy_x_ptr = enemy_x
lea enemy_y,a1 ; int16 *enemy_y_ptr = enemy_y
lea enemy_dx,a2 ; int16 *enemy_dx_ptr = enemy_dx
lea enemy_dy,a3 ; int16 *enemy_dy_ptr = enemy_dy
move.w #N-1,d0
.loop ; do
add.w (a2),a0 ; (*enemy_x_ptr) += *enemy_dx_ptr
add.w (a3),a1 ; (*enemy_y_ptr) += *enemy_dy_ptr
add.l #2,a0 ; ++enemy_x_ptr
add.l #2,a1 ; ++enemy_y_ptr
add.l #2,a2 ; ++enemy_dx_ptr
add.l #2,a3 ; ++enemy_dy_ptr
dbra d0,.loop ; while (i < COUNT)
Performance Analysis
The CPU of the Genesis, the Motorola 68000, does not have a cache, caching was only present in the Motorola processors 68010 and newer, so performance on the 68000 only really depends on how many clock cycles a given algorithm uses. Unlike most newer CPUs, memory access patterns are not a factor.
Let's first look at the sequential layout update routine:
lea enemy_data,a0 ; i = 0; enemy e = data[i]
move.w #N-1,d7
.loop ; do
move.w offset_dx(a0),d0 ; e.x += e.dx
add.w d0,offset_x(a0) ;
move.w offset_dy(a0),d0 ; e.y += e.dy
add.w d0,offset_y(a0) ;
add.l #STRUCT_SIZE,a0 ; e = data[++i]
dbra d7,.loop ; while (i < COUNT)
Inside the loop, we have 3 different instructions, excluding the loop code itself:
move.w d(An),Dn ; d(An) - Address register indirect, displacement
; Dn - Data register direct
; - 12 cycles
add.w Dn,d(An) ; Address operand calculations:
; add.w Dn,<M> - 8 cycles
; <M> = d(An) - 8 cycles
; ---------
; 16 cycles
add.l #,An ; = ADDQ.L - 8 cycles
See the Neo-Geo Development Wiki for more on MC68000 instruction timing.
Using this information, we know that the meat of the loop uses:
move.w offset_dx(a0),d0 ; 12 cycles
add.w d0,offset_x(a0) ; 16 cycles
move.w offset_dy(a0),d0 ; 12 cycles
add.w d0,offset_y(a0) ; 16 cycles
add.l #STRUCT_SIZE,a0 ; 8 cycles
; ----------------
; total: 64 cycles
In total, the update algorithm takes 64 * N cycles.
If we compare that to the member array implementation:
lea enemy_x,a0 ; int16 *enemy_x_ptr = enemy_x
lea enemy_y,a1 ; int16 *enemy_y_ptr = enemy_y
lea enemy_dx,a2 ; int16 *enemy_dx_ptr = enemy_dx
lea enemy_dy,a3 ; int16 *enemy_dy_ptr = enemy_dy
move.w #N-1,d0
.loop ; do
add.w (a2),a0 ; (*enemy_x_ptr) += *enemy_dx_ptr
add.w (a3),a1 ; (*enemy_y_ptr) += *enemy_dy_ptr
add.l #2,a0 ; ++enemy_x_ptr
add.l #2,a1 ; ++enemy_y_ptr
add.l #2,a2 ; ++enemy_dx_ptr
add.l #2,a3 ; ++enemy_dy_ptr
dbra d0,.loop ; while (i < COUNT)
We have 2 different instructions, excluding the loop code itself:
add.w (An),An ; Address operand calculations:
; add.w <ea>,An - 8 cycles
; <ea> = (An) - 4 cycles
; 12 cycles
add.l #,An ; = ADDQ.L - 8 cycles
Now, we can calculate the total cycle count:
add.w (a2),a0 ; 12 cycles
add.w (a3),a1 ; 12 cycles
add.l #2,a0 ; 8 cycles
add.l #2,a1 ; 8 cycles
add.l #2,a2 ; 8 cycles
add.l #2,a3 ; 8 cycles
; ------------
; total: 56 cycles
In total, the update algorithm takes 56 * N cycles, so in this case, the member array approach is somewhat faster. It is mainly due to avoiding the use of 'Address register indirect with displacement', which is a bit slow.
Function Calling Conventions

In many programming languages, parsing parameters into and out of functions and methods is hidden by the language implementation. For example, the formal parameters may be pushed onto the stack by the calling code before giving executing to the function body itself. In assembly code, you have to make these decisions yourself.
The simplest implementation would be defining input and output registers for a function:
result = Add(parameterA, parameterB)
D0 D0 D1
This function could be implemented like this:
Add:
add.w D1,D0
rts
And called like this:
; D0 = Add(5,7)
move.w #5,D0 ; parameterA = 5
move.w #7,D1 ; parameterA = 7
jsr Add
This works, as long as you're careful with which registers are overwritten by functions.
However, when you have multiple levels of function calls, it goes bad almost immediately:
Multiply:
move.w d0,d2 ; Multiply destroys D2
.loop:
add.w d2,d0
dbra d1,.loop
rts
; result = Power( x, power )
; D0 D0 D1
Power:
move.w d1,d2 ; But D2 is also used by Power... Uh oh
.loop:
move.w d2,d0
jsr Multiply ; When this is done, D2 is destroyed
dbra d2,.loop ; argh
rts
To avoid problems, our function can save the state of the registers that will be overwritten onto the stack:
Multiply:
move.l d1,-(sp) ; push D1 onto stack
move.l d2,-(sp) ; push D2 onto stack
move.w d0,d2 ; destroys D2, but we already saved it
.loop:
add.w d2,d0
dbra d1,.loop ; here we subtract from D1
; Restore D1 and D2 from the stack.
; Since we pushed D1 before D2, we must pop them
; in the opposite order:
move.l (sp)+,d2 ; restore D2 from the stack
move.l (sp)+,d1 ; restore D1 from the stack
rts
We can use the 'movem' instruction to save and restore multiple registers:
movem.l d1-d2,-(sp) ; push d1, d2 to the stack
movem.l (sp)+,d1-d2 ; pop d2, d1 from the stack
If you don't wan't to figure out which registers are overwritten, you can save and restore all of them:
movem d0-d7/a0-a6,-(sp) ; push all registers onto the stack
movem (sp)+,d0-d7/a0-a6 ; restore all registers from the stack
It's obviously faster to only push the ones you actually overwrite.
State Pattern
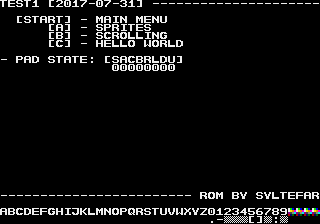
I wanted to implement a State Pattern in 68000 assembly to make a menu structure. My first implementation is based on the way I would implement it in C#, like this:
delegate void StateMethod();
void Test() {
StateMethod state = StateA;
state();
}
void StateA() { }
void StateB() { }
The 68000 assembly version could look like this:
state = $E00000 ; function ptr location
move.l #StateA,state ; state = StateA
.loop;
move.l state,a0 ; a0 = *(state)
jsr (a0) ; jumps to a0, call StateA
bra .loop
StateA:
rts
StateA:
rts
I found an equivalent implementation in the disassembled code of Sonic the Hedgehog, which was based on a jump table:
MainGameLoop:
move.b (v_gamemode).w,d0 ; load Game Mode
andi.w #$1C,d0
jsr GameModeArray(pc,d0.w) ; jump to apt location in ROM
bra.s MainGameLoop
GameModeArray:
ptr_GM_Sega: bra.w GM_Sega ; Sega Screen ($00)
ptr_GM_Title: bra.w GM_Title ; Title Screen ($04)
ptr_GM_Demo: bra.w GM_Level ; Demo Mode ($08)
ptr_GM_Level: bra.w GM_Level ; Normal Level ($0C)
ptr_GM_Special: bra.w GM_Special ; Special Stage ($10)
ptr_GM_Cont: bra.w GM_Continue ; Continue Screen ($14)
ptr_GM_Ending: bra.w GM_Ending ; End of game sequence ($18)
ptr_GM_Credits: bra.w GM_Credits ; Credits ($1C)
rts
Based on that, here is a jump table implementation of the state pattern:
move.w #0,d0 ; function index = 0 (StateA)
lsl.w #2,d0 ; d0 *= sizeof( function pointer ) = 4
jsr DoState(pc,d0.w) ; invoke jump table
DoState: ; Jump table
bra.w StateA ; offset 0
bra.w StateB ; offset 4
rts ; this should never be reached
StateA:
rts
StateB:
rts
I ended up using the jump table, as adding new functions was trivial compared to assigning new function pointers.