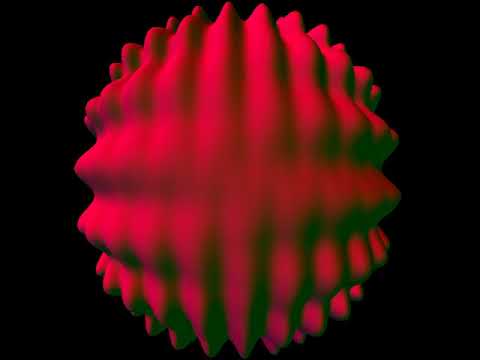
Video
The shape is defined as a signed distance field (SDF), a function that for every point P returns the distance to the surface of the shape. A positive value defines the exterior of the surface, 0 defines the surface itself, and negative values are inside the surface.
The shape is derived from the SDF of a sphere. The SDF below returns a value for every point in 3D space P, signifying the distance to the surface of a sphere placed at the point C with a radius of r:
sphere(P) = distance(P, C) - r P,C ∈ ℝ³ , r ∈ ℝ
The shape is then modified by displacing the center of the sphere based on the position of P, which warps the surface shape:
shape(P) = distance(P, warp(P)) - r
The warp function is based on the x and y coordinates of P, with constants ω and 'strength' denoting a frequency and amplitude of a sinusoid displacement, respectively:
[ sin( ω P.y ) strength ]
warp(P) = [ sin( ω P.x ) strength ] ω,strength ∈ ℝ
[ 2 ]
The shape is animated by adding a time parameter t (seconds):
shape(P, t) = distance(P, warp(P, t)) - r
The warp function is frequency and amplitude modulated by two sinusoids for both x and y, with modulation frequencies fmf0, fmf1, amf0, and amf1:
[ sin( ω P.y sin( fmf0 t ) ) strength sin( amf0 t ) ]
warp(P,t) = [ sin( ω P.x sin( fmf1 t ) ) strength sin( amf1 t ) ] amf0,amf1,fmf0,fmf1 ∈ ℝ
[ 2 ]
This is implemented in a straightforward way in GLSL, replacing constants with numbers:
float sdf(vec3 p)
{
return distance(p, vec3(
sin( p.y * sin(2.0 * time) * 20.0 ) * sin( 5.0 * time ) * 0.2,
sin( p.x * sin(2.7 * time) * 20.0 ) * sin( 3.0 * time ) * 0.2,
2.0))
- 2.0;
}
The ray marching algorithm steps into the from a point through a screen pixel. This code is run for every pixel:
vec3 pos = vec3(vPosition.x, vPosition.y, 0.0);
vec3 dir = pos - vec3(0.0, 0.0, -1.0);
// ray marching
float d = 10.0;
for(int i =0; i < 256; i++)
{
d = sdf(pos);
pos += direction * d;
if(d < 0.02 || pos.z > 100.0) break;
}
// close enough to sphere: white, otherwise black
vec3 col;
if(d<=0.02) gl_FragColor = vec3(1,1,1);
else gl_FragColor = vec3(0,0,0);
The full shader code is here:
void main(void)
{
vec3 pos = vec3(vPosition.x, vPosition.y, 0.0);
vec3 dir = pos - vec3(0.0, 0.0, -1.0);
// ray marching
float d = 10.0;
for(int i =0; i < 256; i++)
{
d = sdf(pos);
pos += direction * d;
if(d < 0.02 || pos.z > 100.0) break;
}
float r = 0.0, g = 0.0, b = 0.0;
if(d<=0.02)
{
// estimate normal based on finite difference approximation of gradient
vec3 gradient = sdf(pos) - vec3(
sdf(pos + vec3(.001,.000,.000)),
sdf(pos + vec3(.000,.001,.000)),
sdf(pos + vec3(.000,.000,.001))
);
vec3 normal = normalize( gradient );
r = dot( normal, normalize( vec3( 0.5,-0.5, 0.5)) ) * 1.0; // red light
g = dot( normal, normalize( vec3(-0.4, 0.4, 0.4)) ) * 0.2; // green light
b = dot( normal, normalize( vec3( 0.9,-0.3, 0.4)) ) * 0.3; // blue light
}
gl_FragColor = vec4(r, g, b, 1.0);
}